Un morceau de bois cylindrique de hauteur \(H=3cm\) flotte à la surface de l’eau. La masse volumique du bois est de \(410 \ kg/m^3\) et celle de l’eau \(1000 \ kg/m^3\). Calculez la hauteur y immergée du bois dans l’eau ?
Schéma:
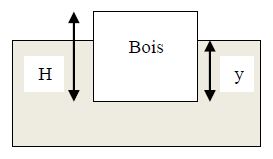

Rapellons premièrement la formule de la poussée d'Archimède.
\[ {\vec {P}}_{\rm {A}}=-\,\rho \,V\,{\vec {g}} \]
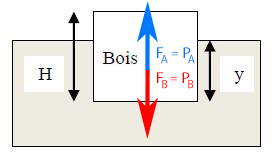
Il nous est dit que le solide flotte à la surfec de l'eau. Dès lors son poids est équilibré par la poussée d'Archimède.
\[ {P}_{\rm {A}}= \ {P}_{\rm {B}} \]
Avec la poussée d'archimède étant égale à :
\[ {P}_{\rm {A}}=\,\rho_{eau} \ . V_{immergé}\ . {g} \]
Et son poids étant égal à :
\[ {P}_{\rm {B}}=\,\rho_{bois} \ .V_{bois}\ . {g} \]
Ce qui nous permet d'isoler le volume immergé qui vaut donc :
\[ V_{immergé} = \,{\rho_{bois} \over \rho_{eau}} \ .V_{bois}\ \]
Étant donné que l'objet considéré est un cylindre, son voulme est proportionnel à sa hauteur. Le volume du bois se calculant comme \( V_{bois} = \ H \times 2\pi r \) et le volume immergé comme \( V_{i} = \ H_i \times 2\pi r \), nous pouvons diviser de part et d'autre par \( 2\pi r \) car ils sont égaux.
\[ H_{immergée} = \,{410 \over 1000} \ . 3 \ \]
\[ H_{immergée} = \,1,23 \ cm \]
La hauteur immergée est égal à \(1,23 \ cm \).
Conditions générales d'utilisation - Politique de confidentialité